语言基础
0.0简介
1.由C扩展而来,添加面对对象部分
2.结构化语言
3.效率高
4.跨平台性
1.1输入输出
由于是静态语言所以必须有一个main()函数;
每句话以;结尾
需要在代码前几行引入所需要的头文件
以最简单的hello,world为例
1
2
3
4
5
6
7
|
#include <iostream> //头文件
using namespace std; //命名空间——std就是standard标准的意思(不过某些人不推荐这么写,但是std::也是很麻烦的)
int main(){//注意不要写成mian[doge]
cout << "hello,world!" << endl; // endl作为换行使用
cin.get(); // 避免程序一闪而过,常见如system("pause"),getchar(),但是在oj上不能写哦!还有是使用古董dev c++的时候会贴心的帮你自动暂停哦。
return 0; //返回0作为程序正常运行
}
|
这样一个最基本的代码就完事了,后缀为.cpp
函数的大括号有两种码风
1
2
3
4
5
6
7
|
int main(){
}
int main()
{
}
|
关于cin和cout
1.« **»**不是什么鬼位移(@某诡异的内存),就是个逻辑符,对向哪一侧就把值传递到那一侧。
2.“这里是字符串”,C艹中 ‘XXX’ 表示字符常量,与某py不一样哦。
3.关于cin的输入多个值
cin对于空格不会读取,所以一般都是拿空格作为分割,亦或输入一个回车一下
For example:
1
2
3
4
5
6
7
8
9
10
11
|
#include <iostream>
#include <string> //#include <cstring>
using namespace std;
int main(){
string a,b,c; //必须先声明变量
cin >> a;
cout << a << endl;
cin >> b >> c;
cout << b << c;
system("pause");
}
|
至此hello,world部分就结束了
关于cstring 和 string 的区别:
1.最**的一个是c的一个是c++的(c++引用库不采用xxx.h的方式,由于包含c的库又避免冲突,就变成<cxxxxx>)
2.如上code中的string类型需要string来实现
3.功能不同
4.string .h 头文件定义了一个变量类型、一个宏和各种操作字符数组的函数。
string为字符串类型提供支持和定义,包括单字节字符串(由char组成)的string和多字节字符串(由wchar_t组成)
参考链接
**常用格式控制符 **
%d 读入或输出int变量
%c 读入或输出char变量
%f 读入或输出float变量,输出时保留小数点后面6位
%lf 读入或输出double变量,输出时保留小数点后面6位
%x 以十六进制读入或输出整型变量
%lld 读入或输出long long 变量(64位整数)
%nd(如%4d,%12d) 以n字符宽度输出整数,宽度不足时用空格填充
%0nd ( 如 %04d,%012d )以n字符宽度输出整数,宽度不足时用0填充
%.nf(如%.4f,%.3f) 输出double或float值,精确到小数点后n位
持续读入
1
2
3
4
|
int c;
while((c = cin.get()) != EOF) {
do something;
}
|
1
2
3
4
|
char c;
while(scanf("%c",&c) != EOF) {
do something;
}
|
1.2基础
1.2.1 数据类型及变量类型
数据类型
| 类型 |
关键字 |
| 布尔型 |
bool |
| 字符型 |
char |
| 整型 |
int |
| 浮点型 |
float |
| 双浮点型 |
double |
| 无类型 |
void |
| 宽字符型 |
wchar_t |
| 类型 |
位 |
范围 |
| char |
1 个字节 |
-128 到 127 或者 0 到 255 |
| unsigned char |
1 个字节 |
0 到 255 |
| signed char |
1 个字节 |
-128 到 127 |
| int |
4 个字节 |
-2147483648 到 2147483647 |
| unsigned int |
4 个字节 |
0 到 4294967295 |
| signed int |
4 个字节 |
-2147483648 到 2147483647 |
| short int |
2 个字节 |
-32768 到 32767 |
| unsigned short int |
2 个字节 |
0 到 65,535 |
| signed short int |
2 个字节 |
-32768 到 32767 |
| long int |
8 个字节 |
-9,223,372,036,854,775,808 到 9,223,372,036,854,775,807 |
| signed long int |
8 个字节 |
-9,223,372,036,854,775,808 到 9,223,372,036,854,775,807 |
| unsigned long int |
8 个字节 |
0 到 18,446,744,073,709,551,615 |
| float |
4 个字节 |
精度型占4个字节(32位)内存空间,+/- 3.4e +/- 38 (~7 个数字) |
| double |
8 个字节 |
双精度型占8 个字节(64位)内存空间,+/- 1.7e +/- 308 (~15 个数字) |
| long double |
16 个字节 |
长双精度型 16 个字节(128位)内存空间,可提供18-19位有效数字。 |
| wchar_t |
2 或 4 个字节 |
1 个宽字符 |
from runoob
变量类型
| 类型 |
描述 |
| bool |
存储值 true 或 false。 |
| char |
通常是一个字符(八位)。这是一个整数类型。 |
| int |
对机器而言,整数的最自然的大小。 |
| float |
单精度浮点值。单精度是这样的格式,1位符号,8位指数,23位小数。 |
| double |
双精度浮点值。双精度是1位符号,11位指数,52位小数。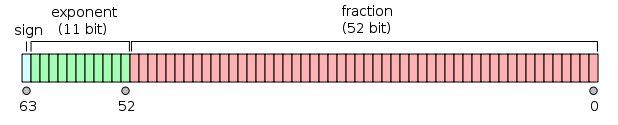 |
| void |
表示类型的缺失。 |
声明一个变量,可以通过
1
2
3
4
5
6
|
类型 变量名 (,变量名,变量名,……);
int a,b,c,d,e,f;
float b;
string abc,woc;//#include <string>
bool haha,xixi;
int a=1,b=2,c=3,d;//还可以同时分别赋值
|
来实现
还可以通过
来实现全局声明
注意:声明和定义并非一体的,以上皆为声明,定义是靠赋值实现的
局部变量可以同时声明定义
1
2
|
int a = 1;
float b = 2.33;
|
而extern则不行
1.2.2常量
常量(可跳过)
1.整数常量
他说我是乱输的啊,我可不是随便输的,这玩意是常量啊
1
2
3
4
5
6
7
|
85 // 十进制
0213 // 八进制
0x4b // 十六进制
30 // 整数
30u // 无符号整数
30l // 长整数
30ul // 无符号长整数
|
2.浮点常量
1
2
3
4
5
|
3.14159 // 合法的
314159E-5L // 合法的
510E // 非法的:不完整的指数
210f // 非法的:没有小数或指数
.e55 // 非法的:缺少整数或分数
|
3.布尔常量
1
2
3
4
5
|
布尔常量共有两个,它们都是标准的 C++ 关键字:
true 值代表真。
false 值代表假。
我们不应把 true 的值看成 1,把 false 的值看成 0。
|
4.字符常量
| 转义序列 |
含义 |
| \ |
\ 字符 |
| ' |
’ 字符 |
| " |
" 字符 |
| ? |
? 字符 |
| \a |
警报铃声 |
| \b |
退格键 |
| \f |
换页符 |
| \n |
换行符 |
| \r |
回车 |
| \t |
水平制表符 |
| \v |
垂直制表符 |
| \ooo |
一到三位的八进制数 |
| \xhh . . . |
一个或多个数字的十六进制数 |
| ‘a’/‘xxxxx’ |
ASCII码 |
5.字符串常量
“字符串”
定义常量
1.#define xxxx xxxx;
相当于全局替换
const T name;
to be contibued
字符串
1.字符串常量 “for example”
2.char[]数组以’\0’结尾,ASCII码是0
- 用char数组存放字符串,数组元素个数应该至少为字符串长度+1
- 使用scanf("%s",A);进行读取 注:无需取地址,因为字符数组相当于指针,本身就指向一个地址
- scanf会自动添加结尾的’\0’
- scanf读入到空格
- 所以如何读入一行呢?
- cin.getline(char buf[], int bufSize); 注:只能存bufsize-1个字符,由于要存’\0’
- char buf[66666];gets(buf); gets从标准输入设备读字符串函数,其可以无限读取,不会判断上限,以回车结束读取,所以应该确保buffer的空间足够大,以便在执行读操作时不发生溢出
- cstring函数
- 字符串拷贝
- strcpy(chardest[],charsrc[]);//拷贝src到dest
- 字符串比较大小
- intstrcmp(char s1[],char s2[]);//返回0则相等
- 求字符串长度
- intstrlen(char s[]);//不算结尾的’\0'
- 字符串拼接
- strcat(char s1[],char s2[]);//s2拼接到s1后面
- 字符串转成大写
- 字符串转成小写
3.c++ STL string : string A;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
|
一. string的构造函数的形式:
string str:生成空字符串
string s(str):生成字符串为str的复制品
string s(str, strbegin,strlen):将字符串str中从下标strbegin开始、长度为strlen的部分作为字符串初值
string s(cstr, char_len):以C_string类型cstr的前char_len个字符串作为字符串s的初值
string s(num ,c):生成num个c字符的字符串
string s(str, stridx):将字符串str中从下标stridx开始到字符串结束的位置作为字符串初值
eg:
string str1; //生成空字符串
string str2("123456789"); //生成"1234456789"的复制品
string str3("12345", 0, 3);//结果为"123"
string str4("012345", 5); //结果为"01234"
string str5(5, '1'); //结果为"11111"
string str6(str2, 2); //结果为"3456789"
二. string的大小和容量:
1. size()和length():返回string对象的字符个数,他们执行效果相同。
2. max_size():返回string对象最多包含的字符数,超出会抛出length_error异常
3. capacity():重新分配内存之前,string对象能包含的最大字符数
三. string的字符串比较:
1. C ++字符串支持常见的比较操作符(>,>=,<,<=,==,!=),甚至支持string与C-string的比较(如 str<”hello”)。
在使用>,>=,<,<=这些操作符的时候是根据“当前字符特性”将字符按字典顺序进行逐一得 比较。字典排序靠前的字符小,
比较的顺序是从前向后比较,遇到不相等的字符就按这个位置上的两个字符的比较结果确定两个字符串的大小(前面减后面)
同时,string (“aaaa”) <string(aaaaa)。
2. 另一个功能强大的比较函数是成员函数compare()。他支持多参数处理,支持用索引值和长度定位子串来进行比较。
他返回一个整数来表示比较结果,返回值意义如下:0:相等 1:大于 -1:小于 (A的ASCII码是65,a的ASCII码是97)
五、string拼接字符串:append() & + 操作符
void test5()
{
// 方法一:append()
string s1("abc");
s1.append("def");
cout<<"s1:"<<s1<<endl; // s1:abcdef
// 方法二:+ 操作符
string s2 = "abc";
/*s2 += "def";*/
string s3 = "def";
s2 += s3.c_str();
cout<<"s2:"<<s2<<endl; // s2:abcdef
}
六、 string的遍历:借助迭代器 或者 下标法
void test6()
{
string s1("abcdef"); // 调用一次构造函数
// 方法一: 下标法
for( int i = 0; i < s1.size() ; i++ )
{
cout<<s1[i];
}
cout<<endl;
// 方法二:正向迭代器
string::iterator iter = s1.begin();
for( ; iter < s1.end() ; iter++)
{
cout<<*iter;
}
cout<<endl;
// 方法三:反向迭代器
string::reverse_iterator riter = s1.rbegin();
for( ; riter < s1.rend() ; riter++)
{
cout<<*riter;
}
cout<<endl;
}
八、 string的字符替换:
1. string& replace(size_t pos, size_t n, const char *s);//将当前字符串
从pos索引开始的n个字符,替换成字符串s
2. string& replace(size_t pos, size_t n, size_t n1, char c); //将当前字符串从pos索引开始的n个字符,替换成n1个字符c
3. string& replace(iterator i1, iterator i2, const char* s);//将当前字符串[i1,i2)区间中的字符串替换为字符串s
string的大小写转换:
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
int main()
{
string s = "ABCDEFG";
string result;
transform(s.begin(),s.end(),s.begin(),::tolower);
cout<<s<<endl;
return 0;
}
string的查找:find
1. size_t find (constchar* s, size_t pos = 0) const;
//在当前字符串的pos索引位置开始,查找子串s,返回找到的位置索引,
-1表示查找不到子串
2. size_t find (charc, size_t pos = 0) const;
//在当前字符串的pos索引位置开始,查找字符c,返回找到的位置索引,
-1表示查找不到字符
3. size_t rfind (constchar* s, size_t pos = npos) const;
//在当前字符串的pos索引位置开始,反向查找子串s,返回找到的位置索引,
-1表示查找不到子串
4. size_t rfind (charc, size_t pos = npos) const;
//在当前字符串的pos索引位置开始,反向查找字符c,返回找到的位置索引,-1表示查找不到字符
5. size_tfind_first_of (const char* s, size_t pos = 0) const;
//在当前字符串的pos索引位置开始,查找子串s的字符,返回找到的位置索引,-1表示查找不到字符
6. size_tfind_first_not_of (const char* s, size_t pos = 0) const;
//在当前字符串的pos索引位置开始,查找第一个不位于子串s的字符,返回找到的位置索引,-1表示查找不到字符
7. size_t find_last_of(const char* s, size_t pos = npos) const;
//在当前字符串的pos索引位置开始,查找最后一个位于子串s的字符,返回找到的位置索引,-1表示查找不到字符
8. size_tfind_last_not_of (const char* s, size_t pos = npos) const;
//在当前字符串的pos索引位置开始,查找最后一个不位于子串s的字符,返回找到的位置索引,-1表示查找不到子串
void test10()
{
char str[] = "I,am,a,student; hello world!";
const char *split = ",; !";
char *p2 = strtok(str,split);
while( p2 != NULL )
{
cout<<p2<<endl;
p2 = strtok(NULL,split);
}
}
https://blog.csdn.net/qq_37941471/article/details/82107077
|
函数传参与运算符重载
函数传参有三种
- 值
- 指针(*)
- 引用(&)
那么区别是什么呢?
传值->传入形参,是原值的拷贝
指针->传入地址
引用->传入实参,是原值的别名
然后众所周知的是我们学的是c with stl而非c++,所以我们只考虑struct就够了
例:
1
2
3
4
5
6
|
struct T{
int a,b;
bool operator< (const T &x)const{
return a<x.a;
}
}
|
但是const是怎么回事呢?
事实上 变量传参是常量传参的子集,也就是说const既可以接收常量,也可以接收变量,所以这么写可以避免出现错误。
ps:前一个const好理解,后一个const是有个暗含的*this
指针
指针作为C的一大利器,也是一大懵逼利器,虽然不用挺多事情也能做(快去tm学python,java),但是这么牛逼怎么能不学学呢.
指针的懵逼之处主要有两点:
1.命名:指针全称指针变量,指针变量的值是指针指向的地址,指针变量经过取值运算后是指向的地址所存储的值,指针的地址是直接经过取地址运算后的值。
2.****的用法: 是取值运算符与取地址运算符&**相对
当声明变量的时候 注意: int * a;此时的*不是运算符,应当理解为 int*是一种变量类型,为整数型指针变量
除此之外含义才是取值运算符
指针的声明
Type * Var;
double * a;//a是指针,a的类型是double *.
指针的取值,变量取地址
1
2
3
4
|
*p;
//*p可以读取从地址P开始的sizeof(T)个字节,T为指针变量的类型,即为声明指针时候的Type
&x;
//&x就是变量x的地址,可以赋值给指针变量
|
指针的运算
1.比较大小(同类型可比较)
1
2
3
|
p1<p2; 等效于 p1指向的地址小与p2指向的地址
p1==p2;
p1>p2'
|
位运算
运算
位运算作为一个十分高效的运算,(尽管反人类)但是能优化空间使用和运算速度,是一大(装逼)利器。
1 Byte(字节) = 8 Bit(比特,位)
| 符号 |
描述 |
运算规则 |
| & |
与 |
两个位都为1时,结果才为1 |
| | |
或 |
任意为1,结果为1 |
| ^ |
异或 |
两个位相同为0,不同为1 |
| ~ |
取反(单目) |
0变1,1变0 |
| « |
左移 |
各二进位全部左移若干位,高位丢弃,低位补0 |
| » |
右移 |
各二进位全部右移若干位,对无符号数,高位补0,有符号数各编译器大多数补符号位(算术右移) |
优先度
| 类别 |
运算符 |
结合性 |
| 后缀 |
() [] -> . ++ - - |
从左到右 |
| 一元 |
+ - ! ~ ++ - - (type)* & sizeof |
从右到左 |
| 乘除 |
* / % |
从左到右 |
| 加减 |
+ - |
从左到右 |
| 移位 |
« » |
从左到右 |
| 关系 |
< <= > >= |
从左到右 |
| 相等 |
== != |
从左到右 |
| 位与 AND |
& |
从左到右 |
| 位异或 XOR |
^ |
从左到右 |
| 位或 OR |
| |
从左到右 |
| 逻辑与 AND |
&& |
从左到右 |
| 逻辑或 OR |
|| |
从左到右 |
| 条件 |
?: |
从右到左 |
| 赋值 |
= += -= *= /= %=»= «= &= ^= |= |
从右到左 |
| 逗号 |
, |
从左到右 |
求int i第n位上的数方法:
ps:然后位运算某奇葩(神犇)用法
可以替代存储0,1的二维数组
补码
在二进制中负数计算时候使用补码
求负整数的补码,将其原码除符号位外的所有位取反(0变1,1变0,符号位为1不变)后加1
e.g.: -5对应带符号位负数5(10000101)→除符号位外所有位取反(11111010)→加00000001(11111011)
二进制枚举
二进制可以很好地表示一个集合内所有的子集是否选择。
1
2
3
4
5
6
7
8
9
10
|
for(int i = 0; i < (1 << n); i++) //从0~2^n-1个状态
{
for(int j = 0; j < n; j++) //遍历二进制的每一位
{
if(i & (1 << j))//判断二进制第j位是否存在
{
printf("%d ",j);//如果存在输出第j个元素
}
}
}
|
高精度
加法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
#include <iostream>
#include <algorithm>
#include <string>
#define MAX 306
int a[MAX],b[MAX],c[MAX];
using namespace std;
int main(){
string A,B;
cin >> A >> B;
int lena=A.length();
int lenb=B.length();
// 使用字符串读入两个大数
for(int i=lena-1,j=0;i>=0;i--,j++){
a[i]=A[j]-'0';
}
for(int i=lenb-1,j=0;i>=0;i--,j++){
b[i]=B[j]-'0';
}
//将大数存在数组当中
int len=max(lena,lenb);
//确认和的长度,如果第一位相加大于10,后续还需要加1
int sum;
for(int i=0;i<=len-1;i++){
sum=a[i]+b[i];
c[i]=sum%10;
c[i+1]=sum/10;
}
//竖式计算
if(c[len]) //除了0之外全是真
len++;
//如果进位,长度加一
for(int i=len-1;i>=0;i--){
cout << c[i];
}
//进行输出
return 0;
}
|
是靠模拟竖式运算实现的,思想很简单,但是写起来bug很多,需要慢慢debug
思路
1.通过string来读取输入的两个大数(需要#include <string>)
2.通过 字符串.length()来读取长度
3.倒序存储数字,事实上没看见过解释这里的,其实主要就是符合从个位开始相加和数组从零开始的惯性思维
4.然后就是相加,通过求10的模来确保这一位是一位数,通过c特有的整数相除取整/10来模拟进位
5.需要判断是否和的长度大于输入两个数的长度,若大于则需要将长度+1,其实此时数组已经存储了多出的这一位(毕竟妹有越界),只是为了输出的时候不落下这一位
6.输出的时候由于是逆序存入,也需要逆序输出
注意事项:这个算法难度很小,但易错点在于循环的次数和数组的下标
1.存入的时候需要从长度-1开始存,到0结束
2.循环可以记成两个端点为len-1和0,条件是>=或<=
排序
sort + 重载运算符 yyds
贪心
(一种鼠目寸光却仍能最优的神奇算法
区间问题
-
取右侧点情况
求区间最多交点
最大不相交区间数量
-
取左侧点
区间分组
区间覆盖
huffman树
优先合并最小的两项
快速幂
1
2
3
4
5
6
7
8
9
10
11
12
|
int fp(int a,int b)//fast power
{
int res=1;
a=a%mod;
while(b)
{
if(b&1) res=(res*a)%mod;
a=(a*a)%mod;
b>>=1;
}
return res;
}
|
分解质因数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
int prime[n];
void divide(int n) {
for(int i = 2; i <= n / i; i++) {
if(n % i == 0) {
while(n % i == 0) {
primes[i]++;
n /= i;
}
}
}
if(n > 1) {//质数本身是自己的质因数
primes[n]++;
}
}
|
二叉堆
此处为小根堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e6+6;
int h[N], size;
void up(int x){
while(x / 2 && h[x] < h[x/2]){
swap(h[x], h[x/2]);
x /= 2;
}
}
void down(int u)
{
int t = u;
if (u * 2 <= size && h[u * 2] < h[t]) t = u * 2;
if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1; //注意此处是h[t],所以确保最终t为最小子树节点
if (u != t)
{
swap(h[u], h[t]);
down(t);
}
}
int main(){
int n, op, x;
scanf("%d", &n);
while (n--)
{
scanf("%d", &op);
switch (op)
{
case 1:
scanf("%d", &x);
h[++size] = x;
up(size);
break;
case 2:
printf("%d\n", h[1]);
break;
case 3:
h[1] = h[size];
size --;
down(1);
break;
}
}
}
|
链式前向星
使用双重vector的邻接表常数大,所以不开o2很虚啊
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
#include <iostream>
using namespace std;
const int N = 1e5;
int head[N], nxt[N], to[N], w[N], idx;
/*
head[i] 最后一个以i为起点的边的下标
nxt [i] 同一起点的边,以i为下标的下一条边
to 以i为下标的边指向的点
w[i] 权重
idx 分配给边的地址,从1 ~ m
*/
void add(int u, int v, int weight = 0){
to[++idx] = v;
w[idx] = weight;
nxt[idx] = head[u];
head[u] = idx;
}
bool find_edge(int u, int v){
for(int i = head[u]; i; i = nxt[i]){
if(to[i] == v)
return true;
}
return false;
}
int main(){
int n, m;
cin >> n >> m;
for(int i = 1; i <= m; i++){
int u , v;
cin >> u >> v;
add(u, v);
}
while(cin >> n && n != 114514){
int u, v;
cin >> u >> v;
cout << find_edge(u, v) << endl;
}
}
|
最短路
最短路分为
1.单源最短路
- 无负权边
- dijkstra算法 用于稠密图
- 堆优化的dijkstra算法 用于稀疏图
- 有负权边
2.多源多汇最短路
朴素dijkstra
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 505;
int g[N][N], d[N], n, m, src; //邻接矩阵存图
bool s[N]; //是否确认最短
void dijkstra() {
memset(d, 0x3f, sizeof d);
d[src] = 0;
for(int k = 1; k < n; k++) { //只是一个无情的计数器,由于源点是手动插入的所以少循环一次
int t = 0;
for(int i = 1; i <= n; i++)
if(!s[i] && (t == 0 || d[i] < d[t]))
t = i;
s[t] = true;
//从t更新
for(int i = 1; i <= n; i++)
d[i] = min(d[i], d[t] + g[t][i]);
}
}
int main() {
//freopen("tmp.in", "r", stdin);
int a, b, c;
scanf("%d%d%d", &n, &m, &src);
//init
memset(g, 0x3f, sizeof g);
for(int i = 1; i <= m; i++) {
scanf("%d%d%d", &a, &b, &c);
g[a][b] = min(g[a][b], c);
}
dijkstra();
for(int i = 1; i <= n; i++) cout << d[i] <<" ";
return 0;
}
|
堆优化dijkstra
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
#include <iostream>
#include <queue>
#include <cstring>
#include <algorithm>
using namespace std;
typedef pair<int,int> PII;
int n, m, src;
const int N = 2e5+6;
int head[N], to[N], w[N], ne[N], idx;
bool vis[N];
int dist[N];
void add (int a, int b, int c) {
to[++idx] = b;
w[idx] = c;
ne[idx] = head[a];
head[a] = idx;
}
void dijkstra() {
memset(dist, 0x3f, sizeof dist);
dist[src] = 0;
priority_queue<PII, vector<PII>, greater<PII> > q;
//greater运算符重载是按照pair的第一个关键词排序的——所以后面的插入元素必须是距离+节点编号
q.push({0, src});
while(q.size()) {
auto t = q.top();
q.pop();
int dest = t.second, distance = t.first;
if(vis[dest])continue;
vis[dest] = true;
for(int i = head[dest]; i; i = ne[i]) {
int j = to[i];
if(dist[j] > distance + w[i]) {
dist[j] = distance + w[i];
q.push({dist[j], j});
}
}
}
}
int main(){
//freopen("tmp.in", "r", stdin);
cin >> n >> m >> src;
for(int i = 1; i <= m; i++){
int a, b ,c;
cin >> a >> b >> c;
add(a,b,c);
}
dijkstra();
for(int i = 1; i <=n ; i++){
if(dist[i] != 1061109567)
cout << dist[i] <<" ";
else
cout << "2147483647 " ;
}
}
|

